前言

在機器學習和深度學習中，損失函數 ( Loss Function ) 是一種用來衡量模型預測值與實際目標之間差異的函數，模型經過損失函數的計算後就會知道模型本身的損失 Loss ( 不準確度 )，損失值越高的模型就愈不準確，越低則越準確，損失函數可以說是判定模型好壞的標準，而模型的訓練就是不斷地計算模型的損失再讓優化器 ( Optimizer ) 用梯度下降 ( Gradient Descent ) 最小化模型的損失，以降低模型的誤差來達到優化模型的目的，損失函數也有分很多種，之間的選擇取決於問題 ( task ) 的性質，不同的 task 會用到不同的損失函數去評估模型好壞，像是回歸問題與分類問題就會用不同的損失函數，下面是常見的損失函數：

均方誤差 Mean Squared Error，MSE

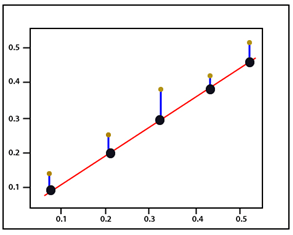
MSE 是計算預測值與實際值之間平方誤差的平均值，MSE 計算方式為將每個實際值減去相應的預測值，然後取絕對值，最後取平均值。公式如下：

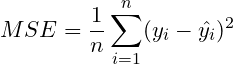
這邊 是樣本數， 是實際值 ( 上圖棕點 )， 是模型的預測值 ( 上圖黑點 )，因為距離不為負， 後需再取平方，最後再取平均值。

均方根誤差 Root Mean Squared Error，RMSE

RMSE 即把 MSE 結果開根號，這便使得 RMSE 的結果值與原始數據 ( ) 的單位一致，讓評估誤差的大小更加直觀，公式如下：

平均絕對誤差 Mean Absolute Error，MAE

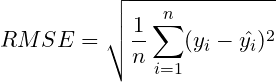
MAE 計算方式為將每個實際值 減去相應的預測值 ，然後取絕對值，最後取平均值，實現衡量預測值和實際值之間的平均誤差。

資訊熵 Information Entropy

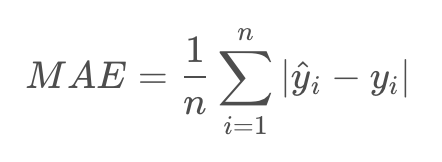
資訊量，看似抽象的東西，其實是可以被量化計算的，指在一個事件中，對我們來說新鮮或意外的資訊的量度，當一個事件的發生是不太常見的，或者與我們預期的相反，它會帶來更多的資訊量。

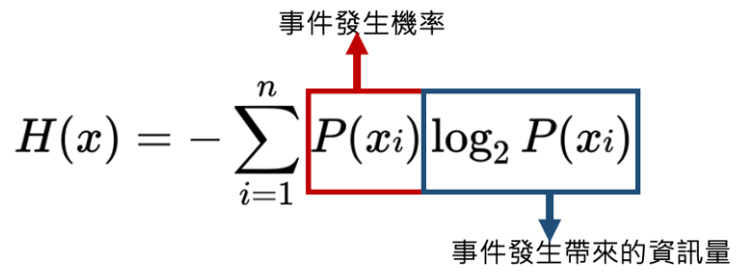
在生活中，舉例來說，新聞每天高機率都在播報車禍事件，這種資訊對我來說可能較不意外，但若突然哪天新聞播出最喜愛的明星爆出醜聞，顯然這種資訊是罕見機率小的，對我來說就很意外，帶給我的資訊量就比較大，一件事情的意外程度便決定了資訊量度的大小，資訊熵即是資訊量度的計算規則，在機器學習中扮演損失函數的角色，計算公式為：

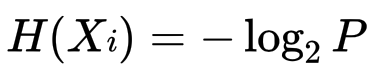
代表一件事的發生， 為該事件發生的機率。

假設過去丟擲 64 次硬幣，有 63 次為正面，僅 1 次為反面，那 63 / 64 即為正面 的機率

• 若下一次再丟一次硬幣為正面，所帶來的資訊量為：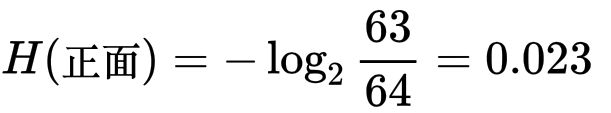
  

• 為反面時，帶來的資訊量為：

• 因此定義資訊熵就是資訊雜亂程度的量化，公式為：

• 當丟硬幣正反兩面出現機率不相同，正面出現機率較高時，下次丟硬幣的資訊熵約為 0.0116 ( 低 )

• 當硬幣正反兩面機率相同時，下次丟硬幣的資訊熵為 1 ( 高 )

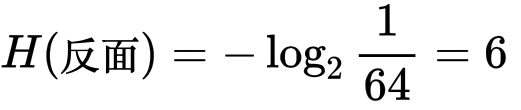
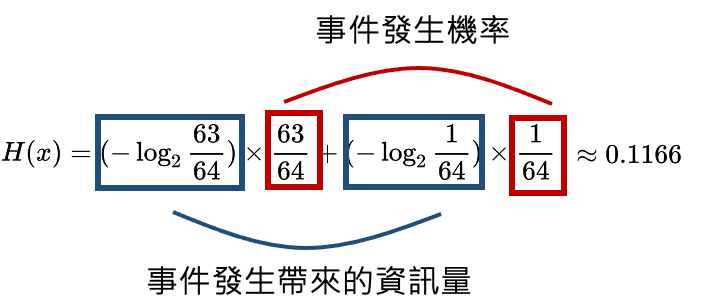
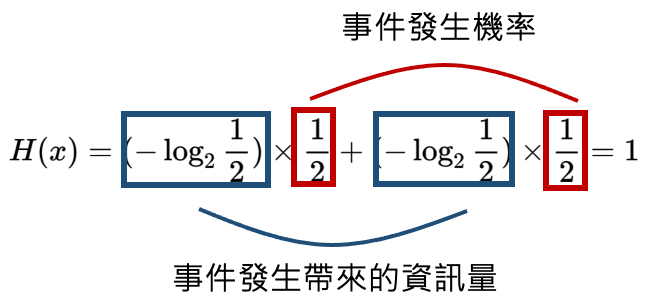
上面結果可以發現：

• 當資料越確定，事件出現機率不同，越能夠預測下次出現的事件，情況越單一，不純度越小，資訊熵越小
• 當資料越不確定，事件出現機率相同，較無法預測下次出現的事件，情況越複雜，不純度越大，資訊熵越大

不純度 Impurity

換種方式講，資訊熵的大小就代表事件 ( 資料 ) 不純度 Impurity ( 不可預測程度 ) 的量化，下圖最右邊，綠色事件發生的機率為 100 %，情況單純， 就為 1，可單純預測下次發生的事即為綠色事件，不純度低，而下圖最左邊，事件發生的機率紅綠各為 50 %，要預測下一次發生哪個事件時，情況就變得不單純且困難，不可預測程度高，不純度高。

決策樹 Decision Tree 的應用

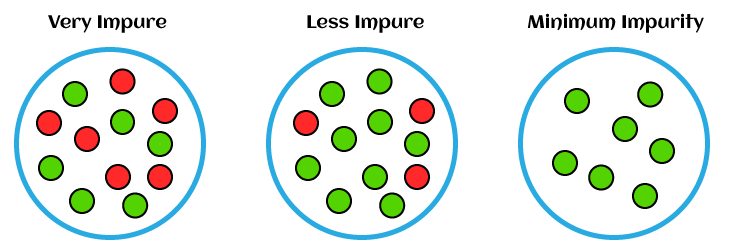
決策樹模型中的損失函數就用了資訊熵的概念，模型優化過程中盡可能降低資訊熵大小，也就是降低資料的不純度，假設在監獄裡面，你用衣服的顏色當決策條件，白衣就是一般犯，黃衣為重罪犯來劃分囚犯牢房，但你若是用身高當作決策條件來劃分牢房，有可能會出現一般犯和重罪犯被關在同一間牢房的情況 ( 資料不純度高 )，所以為了確保牢房關的都是同一類囚犯 ( 不純度低 )，決策樹目標就是用特徵資料做為決策條件，完美區分資料 ( 囚犯 )，讓被區分後的資料 ( 可能不只一個 ) 不純度低，前面也有提到資訊熵就像是對一件事的意外程度，因此只要降低資訊熵低，就能降低模型預測結果的意外程度。

交叉熵與多元分類問題

交叉熵 ( Cross Entropy ) 也是一種損失函數，常應用在多元分類的問題，假設有 個類別 ( 標籤 )，對於每個樣本，模型會輸出 維的預測機率向量 ，其中 代表預測屬於第 類的概率，而每個樣本也都有真實標籤，可表為，其中 為第 類的標籤，通常為 0 或 1，要計算真實標籤 和模型預測的機率 之間的交叉熵，公式如下：

交叉熵可視為一種評估模型預測和真實標籤之間差異的指標，並且越小表示模型預測越接近真實資料。

二元交叉熵與二元分類問題

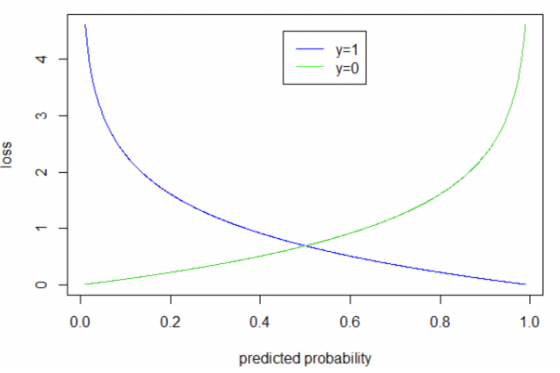
應用在二元分類問題時，會把剛才的交叉熵的公式轉型一下，就變成了二元交叉熵 ( Binary Cross Entropy )，當 =1 時就代到藍色的函數， = 0 就代入綠色函數，可對於不同的樣本資料的標籤 把模型預測結果 代入對應的函數，最後再將所有樣本的 BCE 取平均得到整體的損失，二元交叉熵的公式如下：

小結

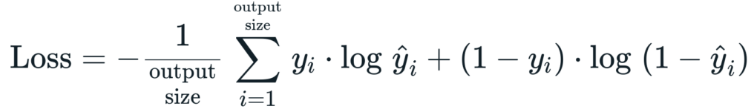
今天我們學習到了：

• 各種損失函數的功能與公式：
  • 均方誤差
  • 均方根誤差
  • 平均絕對誤差
  • 資訊熵
  • 交叉熵
  • 二元交叉熵
• 決策樹中不純度的概念

介紹完各種損失函數後，在下一篇文章中我們就要來介紹機器學習中重要的超參數 - 學習率 ( Learning Rate )，那我們下篇文章見 ~

參考資料

https://www.javatpoint.com/pytorch-mean-squared-error

https://www.cupoy.com/qa/club/ai_tw/0000016D6BA22D97000000016375706F795F72656C656173654B5741535354434C5542/0000017BA07DF516000000076375706F795F72656C656173655155455354

https://androidkt.com/choose-cross-entropy-loss-function-in-keras/

https://www.datasciencepreparation.com/blog/articles/what-is-cross-entropy-loss/